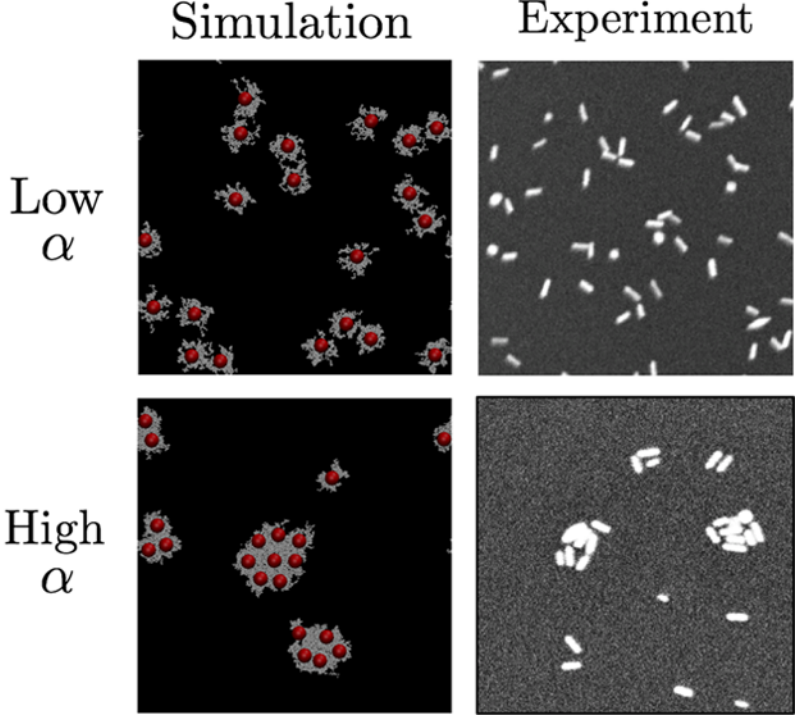
Abstract
Because of the considerable parameter space, efficient theoretical and simulation methods are required to predict the morphology and guide experiments in polymer nanocomposites (PNCs). Unfortunately, theoretical and simulation methods are restricted in their ability to accurately map to experiments based on necessary approximations and numerical limitations. In this study, we provide direct comparisons of two recently developed coarse-grained approaches for modeling polymer nanocomposites (PNCs): polymer nanocomposite field theory (PNC-FT) and dynamic mean-field theory (DMFT). These methods are uniquely suited to efficiently capture mesoscale phase behavior of PNCs in comparison to other theoretical and simulation frameworks. We demonstrate the ability of both methods to capture macrophase separation and describe the thermodynamics of PNCs. We systematically test how the nanoparticle morphology in PNCs is affected by a uniform probability distribution of grafting sites, common in field-based methods, versus random discrete grafting sites on the nanoparticle surface. We also analyze the accuracy of the mean-field approximation in capturing the phase behavior of PNCs. Moreover, the DMFT method introduces the ability to describe nonequilibrium phase behavior while the PNC-FT method is strictly an equilibrium method. With the DMFT method we are able to show the evolution of nonequilibrium states toward their equilibrium state and a qualitative assessment of the dynamics in these systems. These simulations are compared to experiments consisting of polystyrene grafted gold nanorods in a poly(methyl methacrylate) matrix to ensure the model gives results that qualitatively agree with the experiments. This study reveals that nanoparticles in a relatively high matrix molecular weight are trapped in a nonequilibrium state and demonstrates the utility of the DMFT framework in capturing nonequilibrium phase behavior of PNCs. Both the PNC-FT and DMFT framework are promising methods to describe the thermodynamic and nonequilibrium phase behavior of PNCs.